고정 헤더 영역
상세 컨텐츠
본문
그리디(greedy) 알고리즘
매 선택의 순간에서 항상 최적의 선택을 하며, 한 번 선택한 것을 되돌리지 않는 알고리즘
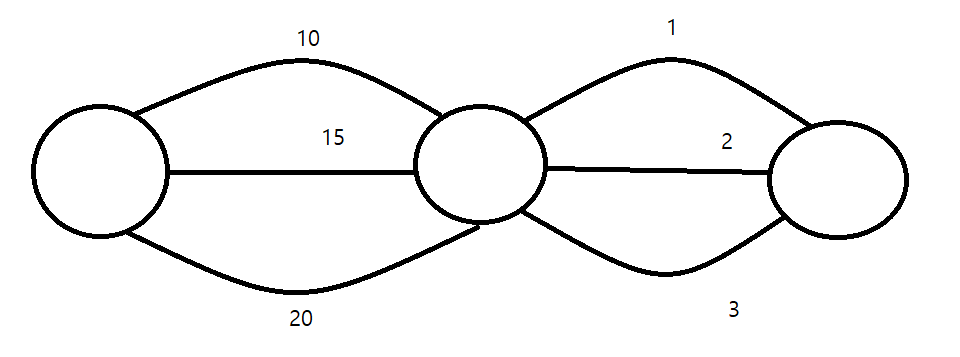
첫 번째 원에서 세 번째 원으로 가는 최단 경로를 구하고 싶다고 하자. 첫 번째 원에서 두 번째 원으로 가는 경우, 반드시 거리가 가장 작은 10을 선택해야 한다. 두 번째 원에서 세 번째 원으로 가는 경우, 반드시 거리가 가장 작은 1을 택해야 한다. 따라서 첫 번째 원에서 세 번째 원으로 가는 최단 경로는 10 + 1 = 11이다.
이 방식에서 매 선택의 순간, 즉 한 원에서 다른 원으로 가는 경로를 택하는 순간에서, 가장 작은 거리를 택하는 최적의 선택을 하여 답을 구했다. 이처럼 매 선택의 순간에서 항상 최적의 선택을 하는 알고리즘을 그리디 알고리즘이라 한다.
단, 매 선택의 순간에서 항상 최적의 선택을 하는 것이 전체적으로 봤을 때 최적의 선택이 아닐 수도 있다.
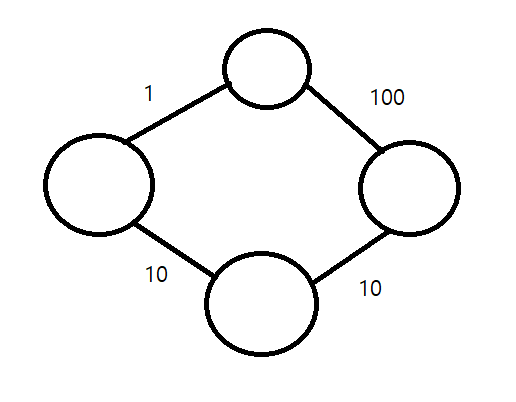
왼쪽 원에서 오른쪽 원으로 이동하는 최단 경로를 구하고 싶다고 하자. 여기에서 최적의 선택을 "현재 원에서 다른 원으로 이동하는 최단 거리"라 한다면, 맨 처음 왼쪽 원에서 위쪽 원으로 이동하는 거리 1을 택해 이동할 것이다. 하지만 그 다음에는 무조건 거리 100을 택해 이동해야 하며, 거리 총합은 1 + 100 = 101이다. 이는 아래쪽 원을 택해 이동하는 거리 10 + 10 = 20 보다 긴 거리이다.
그리디 알고리즘을 제대로 적용하기 위해서는 각 선택이 다른 선택에 영향을 주어서는 안 된다. 만약 영향을 준다면 현재 최적의 선택을 했다 하더라도, 위 예시처럼 전체적으로 봤을 때 최적의 선택이 아닐 수 있기 때문이다.
그리디 알고리즘의 대표적인 문제로 이벤트 스케줄링이 있다.
https://www.acmicpc.net/problem/1931
1931번: 회의실 배정
(1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다.
www.acmicpc.net
이 문제에서 최적의 선택은, 끝나는 시간이 가장 빠른 회의실을 먼저 선택하는 것이다. 만약 끝나는 시간이 가장 빠른 회의실을 선택하지 않는다면, 회의실을 선택할 수 있는 경우의 수가 가장 빠른 회의실을 선택할 경우보다 같거나 적게 된다.
먼저 끝나는 시간 순으로 회의를 정렬한 후, 생각해낸 최적의 선택에 따라 회의실를 배정한다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tiii;
int N;
vector<pii> meeting;
auto cmp = [](pii m1, pii m2)
{
auto [s1, e1] = m1;
auto [s2, e2] = m2;
if (e1 < e2 || (e1 == e2 && s1 < s2))
return true;
else
return false;
};
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> N;
for (int i{1}; i <= N; i++)
{
int s, e;
cin >> s >> e;
meeting.push_back({s, e});
}
sort(meeting.begin(), meeting.end(), cmp);
int ans{0};
int endTime{0};
for (auto [s, e] : meeting)
{
if (endTime <= s)
{
ans++;
endTime = e;
}
}
cout << ans << "\n";
}
그리디 알고리즘은 해결 방법으로 생각해내기 어려운 알고리즘인데, 그 이유를 요약하면 대략 이렇다.
1. 해당 문제를 그리디 알고리즘으로 풀 수 있는가?
2. 이러한 방식의 선택이 최적임을 증명할 수 있는가?
그리디 알고리즘에서 어려움을 겪는 부분은 "최적의 선택"이 무엇인가를 아는 것이다. 위의 두 그림에서는 최적의 선택이 "가장 짧은 거리를 택하는 것"이라는 것을 쉽게 알 수 있다. 하지만 어려운 문제에서는 이것이 바로 보이지 않는데, 이는 곧 이 문제의 해결 방법이 그리디 알고리즘이라는 것을 생각해내기 어렵게 한다. 2번 이유가 1번 이유를 만든 원인이라 봐도 무방한 것이다. 따라서 그리디 알고리즘으로 문제를 해결하기 위해서는, 자신이 생각한 최적의 선택이 정말 최선인가를 증명할 수 있어야 할 것이다.
'알고리즘 > algorithm' 카테고리의 다른 글
| 누적 합(Prefix Sum) (0) | 2023.04.27 |
|---|---|
| 분할 정복(Divide and Conquer) (0) | 2023.04.27 |
| 정수론 - 소수 판정, 에라토스테네스의 체, 유클리드 호제법 (0) | 2023.04.25 |
| 이분 탐색(Binary Search) (0) | 2023.04.24 |
| 도움이 되는 것들 (0) | 2023.04.05 |





댓글 영역